Examen de machine learning

news

Author

Jumbong Junior

Published

December 8, 2023

Introduction

Il est possible que ce soit Da Veiga qui assure vos cours, mais je vais vous offrir un aperçu de ce à quoi pourrait ressembler votre examen. C’est important, car nous avons tendance à sous-estimer ce type d’activité, surtout lorsqu’il autorise l’utilisation de générateurs de texte tels que ChatGPT. Cette année, peu d’étudiants ont achevé le projet, la charge de données étant longue et fastidieuse. Je vous conseille de vous y prendre en avance. Préparez des fonctions exécutant certaines tâches spécifiques, que je vous expliquerai progressivement.

Les données

Les données, très larges proposées sont Dataset1 et Dataset2. Vous les trouverez sur mon github

Packages

J’utiliserai les packages suivants: sklearn, pandas, numpy, matplotlib,seaborn pour la visualiation.

Objectif

L’objectif de ce notebook consistera à une ’analyse exploratoire des données, le prétraitement des données pour la modélisation, et l’application ainsi que l’évaluation de modèles de classification() sur un ensemble de données.

# Importation des packages


import pandas as pd
import numpy as np
import pandas as pd
import chardet
import warnings
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
warnings.filterwarnings("ignore")

from sklearn.model_selection import train_test_split

from sklearn.feature_selection import mutual_info_classif

from sklearn.feature_selection import mutual_info_classif


from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline

from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.metrics import accuracy_score

from sklearn.metrics import confusion_matrix

from sklearn.ensemble import RandomForestClassifier

from sklearn.preprocessing import LabelEncoder
import xgboost as xgb
from xgboost import XGBClassifier

Chargement des données

with open('Dataset1.csv', 'rb') as f:
    result = chardet.detect(f.read())  # or readline if the file is large
#print(result['encoding'])

Dataset1 = pd.read_csv('Dataset1.csv', delimiter=",",decimal = ".",encoding=result['encoding'])
Dataset1.head()

	Vegetation_Type_2	Groundwater_Level_1	Drainage_Quality_1	Slope	Hillshade_9am	Hillshade_Noon	Pollution_Level_1	Water_Source_Distance_2	Terrain_Roughness_2	Urban_Proximity_Index_1	...	Soil_Moisture_Level_2	Horizontal_Distance_To_Hydrology	Wind_Speed_Average_2	Elevation_Range_1	Pollution_Level_2	Vegetation_Type_1	Temperature_Average_1	Canopy_Cover_2	Elevation	Cover_Type
0	450.684968	2054.426315	229.994980	3	221	232	181.000000	227.161401	216.000000	14.0	...	418.375833	258	116.000000	219.000000	224.000000	0.000000	9.000000	503.586301	2596	5
1	889.885392	997.573983	208.000000	2	220	235	166.000000	933.851870	251.000000	16.0	...	2488.726342	212	179.025367	236.000000	224.000000	69.000000	17.000000	537.000000	2590	5
2	1232.738700	676.352745	214.313227	9	234	238	205.000000	4235.282432	176.898683	13.0	...	1852.423116	268	156.000000	200.872578	230.415218	120.357544	10.000000	376.000000	2804	2
3	3359.512595	4720.481538	230.000000	18	238	238	176.002696	1066.935784	220.000000	11.0	...	5388.528248	242	156.000000	230.000000	243.000000	15.000000	12.933234	30.000000	2785	2
4	1907.275049	2187.627994	221.000000	2	220	234	109.000000	1182.489702	184.859965	9.0	...	304.080537	153	112.000000	232.000000	213.000000	39.000000	14.000000	330.000000	2595	5

5 rows × 51 columns

#info
Dataset1.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 581012 entries, 0 to 581011
Data columns (total 51 columns):
 #   Column                              Non-Null Count   Dtype  
---  ------                              --------------   -----  
 0   Vegetation_Type_2                   581012 non-null  float64
 1   Groundwater_Level_1                 581012 non-null  float64
 2   Drainage_Quality_1                  581012 non-null  float64
 3   Slope                               581012 non-null  int64  
 4   Hillshade_9am                       581012 non-null  int64  
 5   Hillshade_Noon                      581012 non-null  int64  
 6   Pollution_Level_1                   581012 non-null  float64
 7   Water_Source_Distance_2             581012 non-null  float64
 8   Terrain_Roughness_2                 581012 non-null  float64
 9   Urban_Proximity_Index_1             581012 non-null  float64
 10  Sunlight_Intensity_2                581012 non-null  float64
 11  Rainfall_Index_1                    581012 non-null  float64
 12  Canopy_Cover_1                      581012 non-null  float64
 13  Rock_Type_2                         581012 non-null  float64
 14  Rainfall_Index_2                    581012 non-null  float64
 15  Terrain_Slope_Angle_2               581012 non-null  float64
 16  Temperature_Average_2               581012 non-null  float64
 17  Air_Quality_Index_1                 581012 non-null  float64
 18  Horizontal_Distance_To_Roadways     581012 non-null  int64  
 19  Soil_Mineral_Content_2              581012 non-null  float64
 20  Wildlife_Density_2                  581012 non-null  float64
 21  Water_Source_Distance_1             581012 non-null  float64
 22  Air_Quality_Index_2                 581012 non-null  float64
 23  Wildlife_Density_1                  581012 non-null  float64
 24  Drainage_Quality_2                  581012 non-null  float64
 25  Land_Use_Category_2                 581012 non-null  float64
 26  Groundwater_Level_2                 581012 non-null  float64
 27  Wind_Speed_Average_1                581012 non-null  float64
 28  Hillshade_3pm                       581012 non-null  int64  
 29  Terrain_Slope_Angle_1               581012 non-null  float64
 30  Land_Use_Category_1                 581012 non-null  float64
 31  Elevation_Range_2                   581012 non-null  float64
 32  Vertical_Distance_To_Hydrology      581012 non-null  int64  
 33  Urban_Proximity_Index_2             581012 non-null  float64
 34  Horizontal_Distance_To_Fire_Points  581012 non-null  int64  
 35  Soil_Mineral_Content_1              581012 non-null  float64
 36  Aspect                              581012 non-null  int64  
 37  Soil_Moisture_Level_1               581012 non-null  float64
 38  Terrain_Roughness_1                 581012 non-null  float64
 39  Rock_Type_1                         581012 non-null  float64
 40  Sunlight_Intensity_1                581012 non-null  float64
 41  Soil_Moisture_Level_2               581012 non-null  float64
 42  Horizontal_Distance_To_Hydrology    581012 non-null  int64  
 43  Wind_Speed_Average_2                581012 non-null  float64
 44  Elevation_Range_1                   581012 non-null  float64
 45  Pollution_Level_2                   581012 non-null  float64
 46  Vegetation_Type_1                   581012 non-null  float64
 47  Temperature_Average_1               581012 non-null  float64
 48  Canopy_Cover_2                      581012 non-null  float64
 49  Elevation                           581012 non-null  int64  
 50  Cover_Type                          581012 non-null  int64  
dtypes: float64(40), int64(11)
memory usage: 226.1 MB

Les données contiennent 51 colonnes et 581012 lignes. Dans le code ci-dessous, nous allons séparer les données en output(Y) et en features(X). L’output ici est la variable Cover_Type.

 # split  data into training and testing sets
X = Dataset1.drop(['Cover_Type'], axis=1).copy()
Y = Dataset1['Cover_Type'].copy()

La prémiere chose à faire est de voir la distribution de Y. Afin de vérifier si c’est une variable catégorielle ou continue.

# Distribution de Y
sns.countplot(x='Cover_Type', data=Dataset1)
plt.show()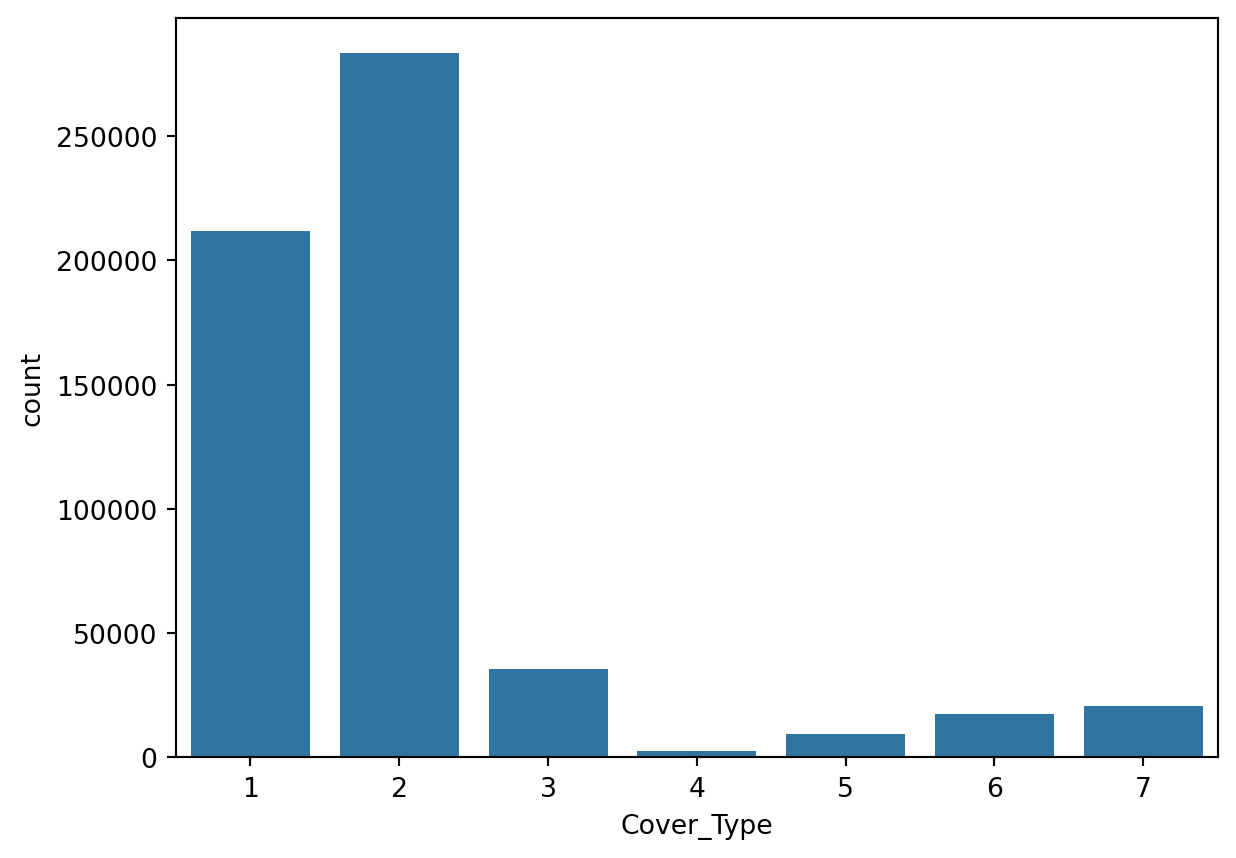

On peut voir que la variable est catégorielle. Elle contient 7 classes non équilibrées. On peut s’attendre que le modèle prédira mieux les classes les plus représentées(1 et 2) que les autres.

Nous ne traiterons pas ça ici. Les données étant labélisées, nous allons utiliser des modèles de classification.

Data preprocessing

Nous pouvons dans un premier temps vérifier s’il y a des valeurs manquantes dans les données.

# Missing values
Dataset1.isnull().sum()

Vegetation_Type_2                     0
Groundwater_Level_1                   0
Drainage_Quality_1                    0
Slope                                 0
Hillshade_9am                         0
Hillshade_Noon                        0
Pollution_Level_1                     0
Water_Source_Distance_2               0
Terrain_Roughness_2                   0
Urban_Proximity_Index_1               0
Sunlight_Intensity_2                  0
Rainfall_Index_1                      0
Canopy_Cover_1                        0
Rock_Type_2                           0
Rainfall_Index_2                      0
Terrain_Slope_Angle_2                 0
Temperature_Average_2                 0
Air_Quality_Index_1                   0
Horizontal_Distance_To_Roadways       0
Soil_Mineral_Content_2                0
Wildlife_Density_2                    0
Water_Source_Distance_1               0
Air_Quality_Index_2                   0
Wildlife_Density_1                    0
Drainage_Quality_2                    0
Land_Use_Category_2                   0
Groundwater_Level_2                   0
Wind_Speed_Average_1                  0
Hillshade_3pm                         0
Terrain_Slope_Angle_1                 0
Land_Use_Category_1                   0
Elevation_Range_2                     0
Vertical_Distance_To_Hydrology        0
Urban_Proximity_Index_2               0
Horizontal_Distance_To_Fire_Points    0
Soil_Mineral_Content_1                0
Aspect                                0
Soil_Moisture_Level_1                 0
Terrain_Roughness_1                   0
Rock_Type_1                           0
Sunlight_Intensity_1                  0
Soil_Moisture_Level_2                 0
Horizontal_Distance_To_Hydrology      0
Wind_Speed_Average_2                  0
Elevation_Range_1                     0
Pollution_Level_2                     0
Vegetation_Type_1                     0
Temperature_Average_1                 0
Canopy_Cover_2                        0
Elevation                             0
Cover_Type                            0
dtype: int64

Il n’y a pas de valeurs manquantes dans les données.

Features selections.

Nous allons supprimer les variables en se basant sur le critère de l’information mutulle qui n’apportent pas au moins 0.01 d’information à la variable cible.

En termes simples, l’information mutuelle mesure combien la connaissance d’une variable réduit l’incertitude concernant l’autre.

mutual_info = mutual_info_classif(X, Y)


mutual_info_df = pd.DataFrame(mutual_info, index=X.columns, columns=['Mutual Information'])

# Filtrer les caractéristiques avec une information mutuelle supérieure à 0.01
relevant_features = mutual_info_df[mutual_info_df['Mutual Information'] > 0.01].index

# Afficher les caractéristiques pertinentes
print("Caractéristiques pertinentes (Information Mutuelle > 0.01) :")
print(relevant_features)

Caractéristiques pertinentes (Information Mutuelle > 0.01) :
Index(['Slope', 'Hillshade_9am', 'Hillshade_Noon',
       'Horizontal_Distance_To_Roadways', 'Hillshade_3pm',
       'Vertical_Distance_To_Hydrology', 'Horizontal_Distance_To_Fire_Points',
       'Aspect', 'Horizontal_Distance_To_Hydrology', 'Elevation'],
      dtype='object')

Nous allons supprimer les variables qui ne sont pas pertinentes.

# Supprimer les caractéristiques non pertinentes
X = X[relevant_features]
X.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 581012 entries, 0 to 581011
Data columns (total 10 columns):
 #   Column                              Non-Null Count   Dtype
---  ------                              --------------   -----
 0   Slope                               581012 non-null  int64
 1   Hillshade_9am                       581012 non-null  int64
 2   Hillshade_Noon                      581012 non-null  int64
 3   Horizontal_Distance_To_Roadways     581012 non-null  int64
 4   Hillshade_3pm                       581012 non-null  int64
 5   Vertical_Distance_To_Hydrology      581012 non-null  int64
 6   Horizontal_Distance_To_Fire_Points  581012 non-null  int64
 7   Aspect                              581012 non-null  int64
 8   Horizontal_Distance_To_Hydrology    581012 non-null  int64
 9   Elevation                           581012 non-null  int64
dtypes: int64(10)
memory usage: 44.3 MB

Là on a plus que 10 features et les données sont toutes numériques.

X.describe()

	Slope	Hillshade_9am	Hillshade_Noon	Horizontal_Distance_To_Roadways	Hillshade_3pm	Vertical_Distance_To_Hydrology	Horizontal_Distance_To_Fire_Points	Aspect	Horizontal_Distance_To_Hydrology	Elevation
count	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000	581012.000000
mean	14.103704	212.146049	223.318716	2350.146611	142.528263	46.418855	1980.291226	155.656807	269.428217	2959.365301
std	7.488242	26.769889	19.768697	1559.254870	38.274529	58.295232	1324.195210	111.913721	212.549356	279.984734
min	0.000000	0.000000	0.000000	0.000000	0.000000	-173.000000	0.000000	0.000000	0.000000	1859.000000
25%	9.000000	198.000000	213.000000	1106.000000	119.000000	7.000000	1024.000000	58.000000	108.000000	2809.000000
50%	13.000000	218.000000	226.000000	1997.000000	143.000000	30.000000	1710.000000	127.000000	218.000000	2996.000000
75%	18.000000	231.000000	237.000000	3328.000000	168.000000	69.000000	2550.000000	260.000000	384.000000	3163.000000
max	66.000000	254.000000	254.000000	7117.000000	254.000000	601.000000	7173.000000	360.000000	1397.000000	3858.000000

analyse exploratoire des données

Pour l’analyse exploratoire, nous allons utiliser qu’un échantillon des données. Je vais en prendre 500

sample_size = 500 # Adjust this based on your dataset size
X_sampled = X.sample(n=sample_size, random_state=42)
Y_sampled = Y.loc[X_sampled.index]
X_sampled.describe()

	Slope	Hillshade_9am	Hillshade_Noon	Horizontal_Distance_To_Roadways	Hillshade_3pm	Vertical_Distance_To_Hydrology	Horizontal_Distance_To_Fire_Points	Aspect	Horizontal_Distance_To_Hydrology	Elevation
count	500.000000	500.000000	500.000000	500.000000	500.000000	500.000000	500.00000	500.000000	500.000000	500.000000
mean	14.642000	211.054000	223.252000	2313.700000	143.338000	46.152000	1906.97800	155.922000	271.758000	2945.782000
std	7.678265	28.780405	19.804366	1548.527391	40.718494	60.782744	1297.58581	111.414732	227.100543	290.643937
min	1.000000	75.000000	149.000000	85.000000	0.000000	-152.000000	42.00000	0.000000	0.000000	1983.000000
25%	9.000000	197.000000	212.750000	1086.250000	119.000000	8.000000	982.75000	59.000000	108.000000	2805.000000
50%	13.000000	217.000000	226.000000	1945.500000	142.000000	29.000000	1642.50000	125.000000	212.000000	3001.000000
75%	19.000000	232.000000	237.000000	3226.250000	171.000000	67.000000	2411.25000	257.000000	376.750000	3149.250000
max	42.000000	253.000000	254.000000	7078.000000	246.000000	387.000000	6576.00000	359.000000	1110.000000	3529.000000

Nous pouvons tracer la distribution de chaque variable.

_ = X_sampled.hist(figsize=(20, 14))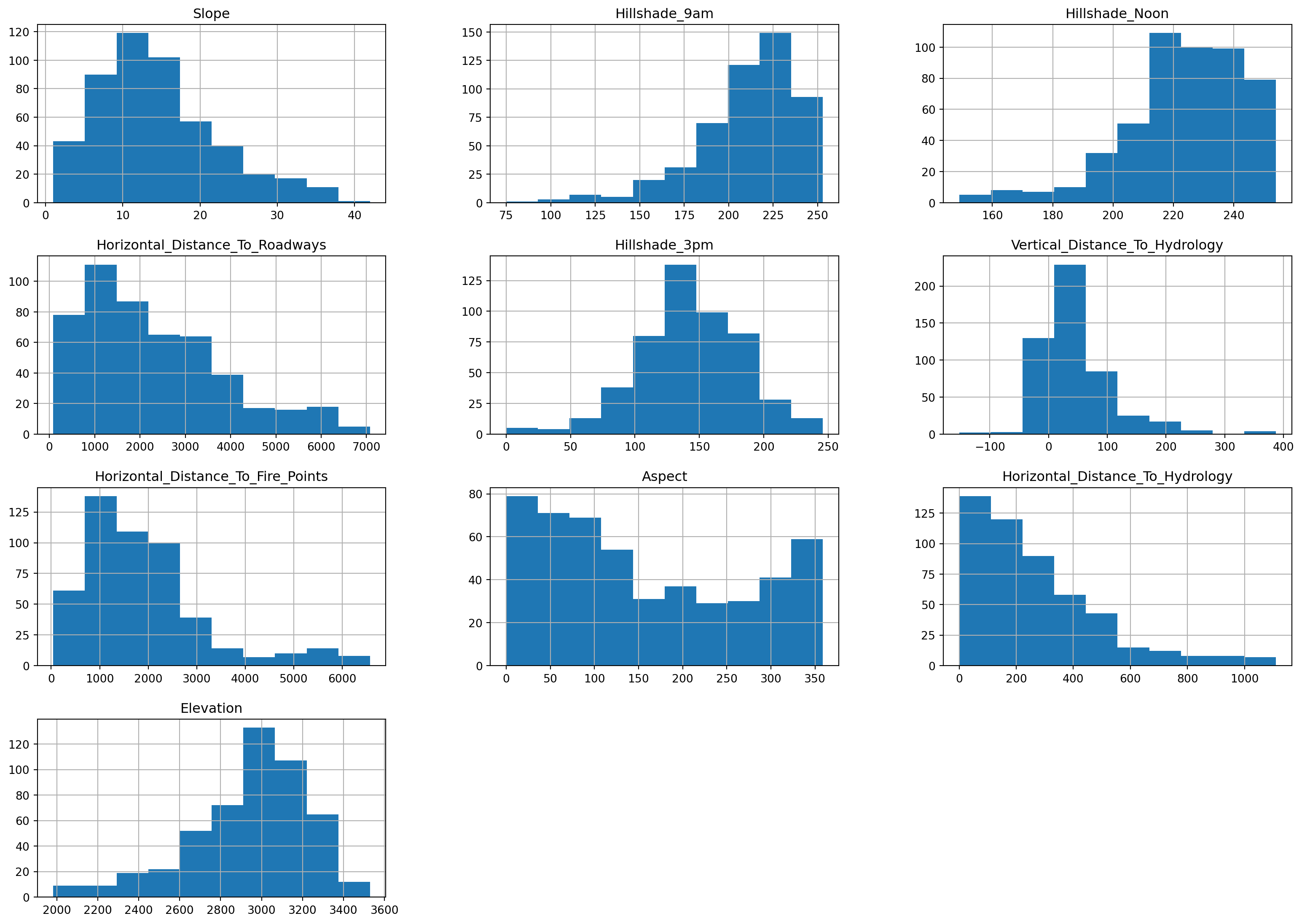

Voyons si on des dinausores dans les données.

sns.pairplot(X_sampled)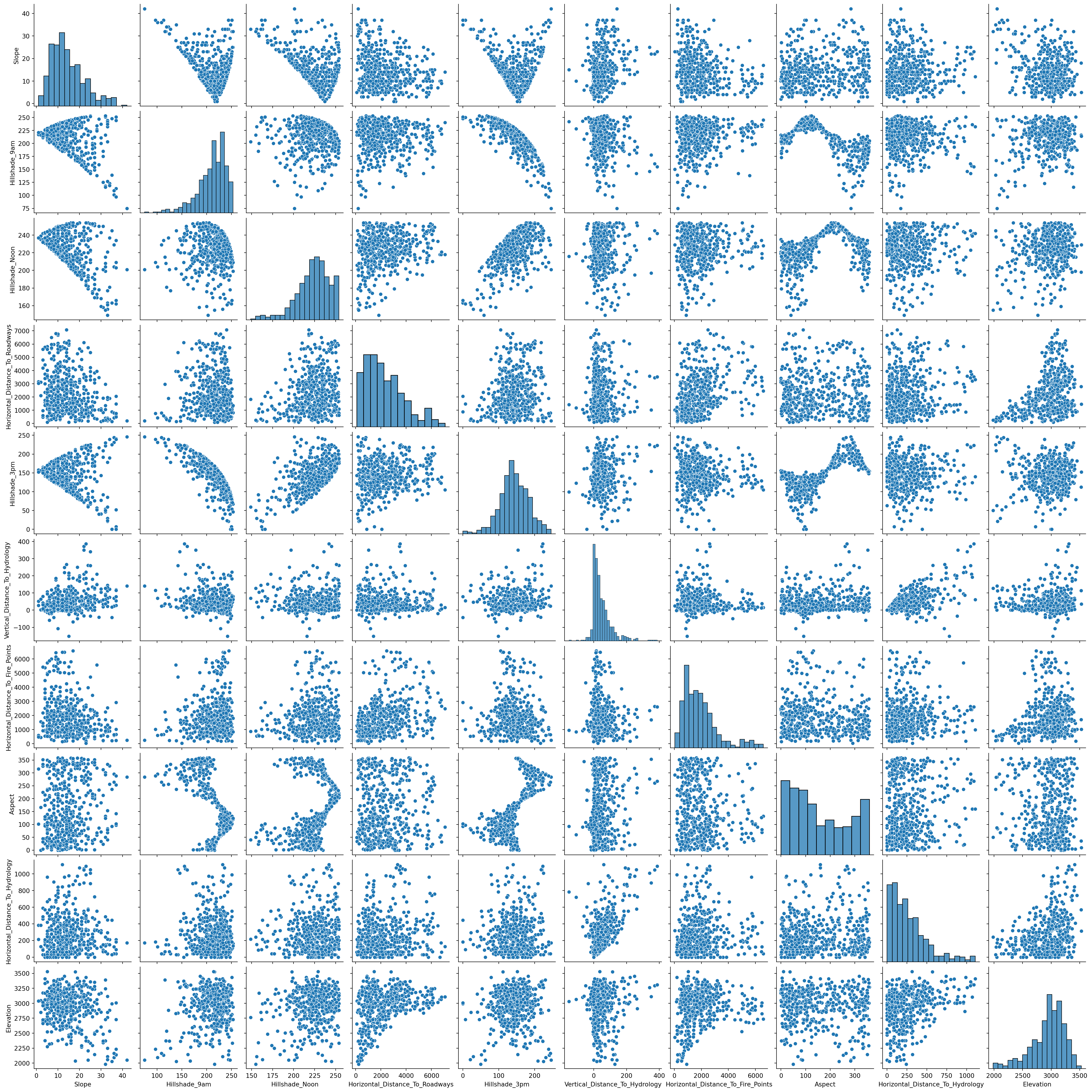

Il semble qu’il n’existe pas de corrélations linéaires entre les variables.

# Correlation matrix
import seaborn as sns
corr_matrix = X_sampled.corr()

# Heatmap of the correlation matrix

_= sns.heatmap(corr_matrix, annot=True)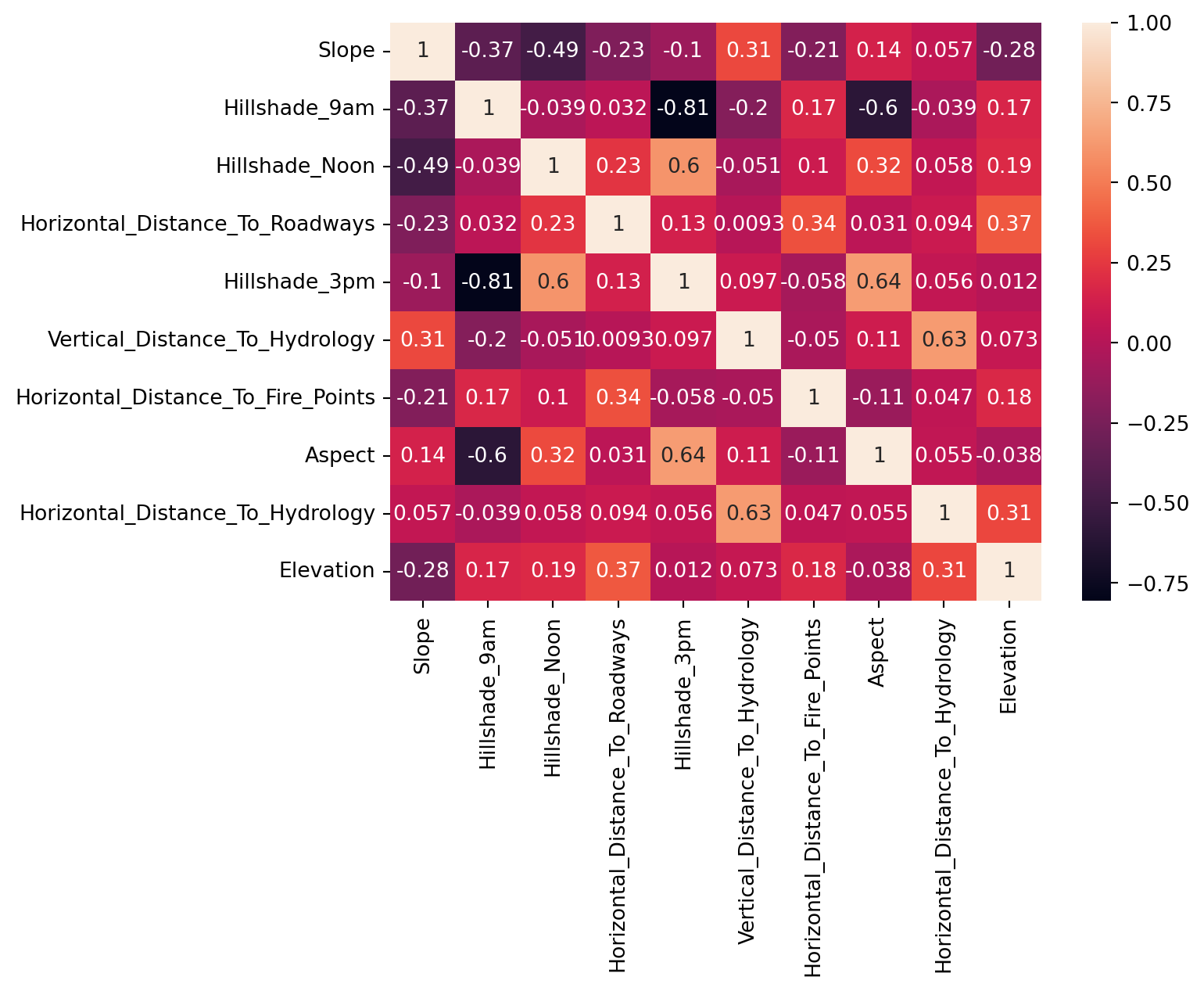

Ce graphique semble confirmer qu’il n’y a pas de corrélations linéaires entre les variables.

Box plot

Le graphique ci-dessous montre la distribution de chaque variable en fonction de la variable cible.

# box plot
# Transformed Cover_Type to categorical
Y_sampled = Y_sampled.astype('category')

for col in X_sampled.columns:
    sns.boxplot(x=Y_sampled, y=X_sampled[col])
    plt.show()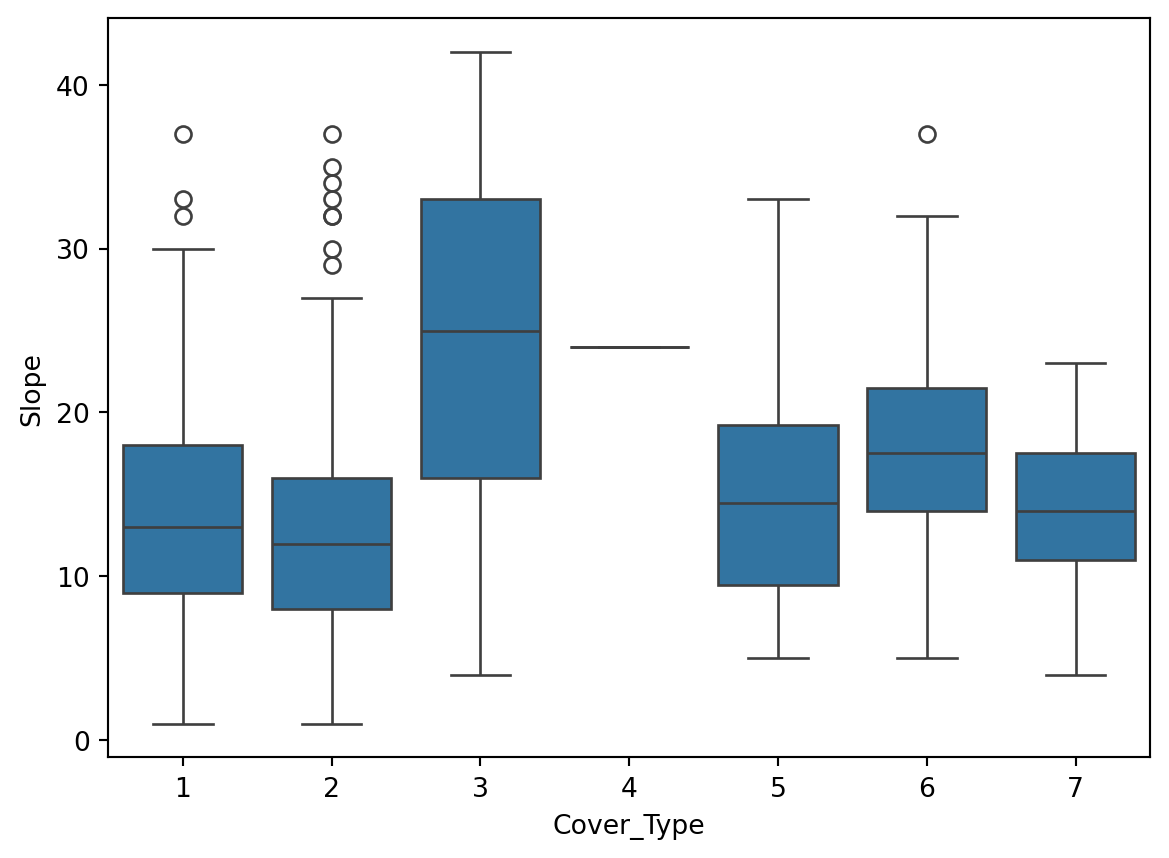

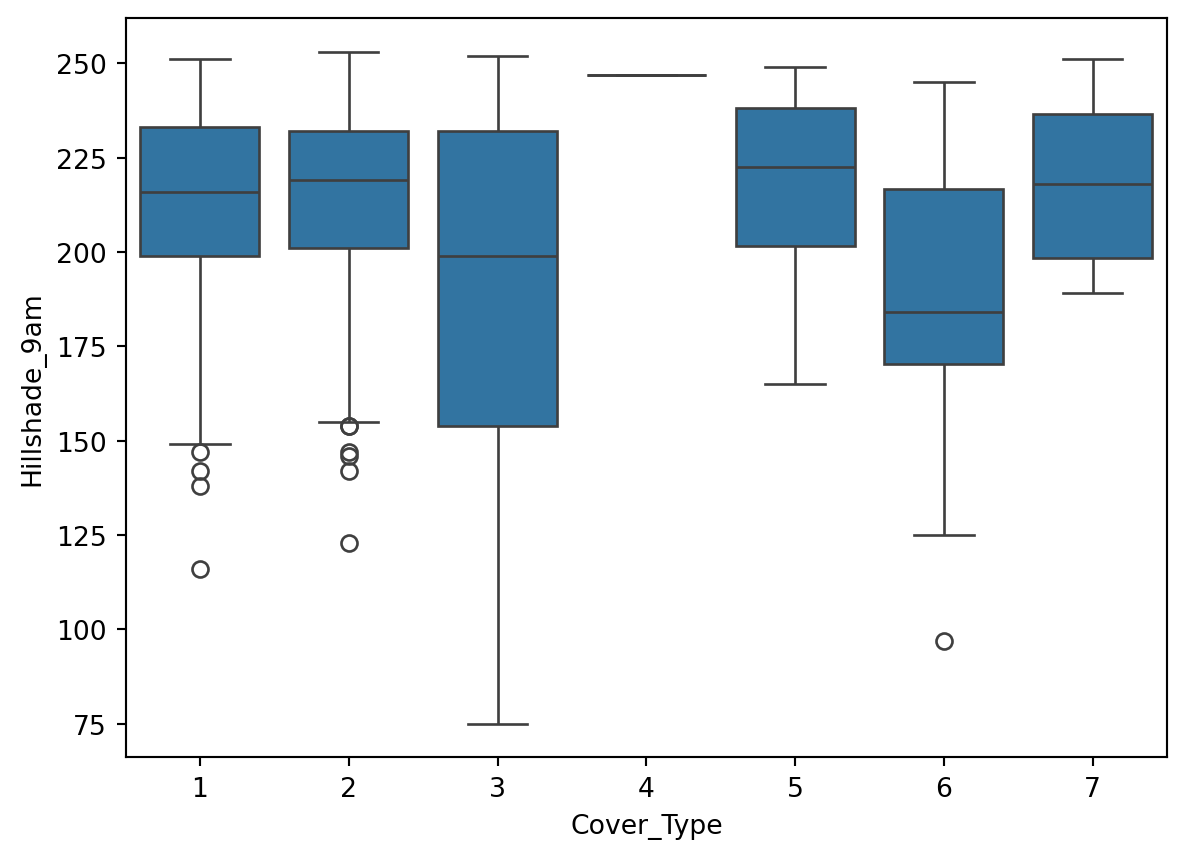
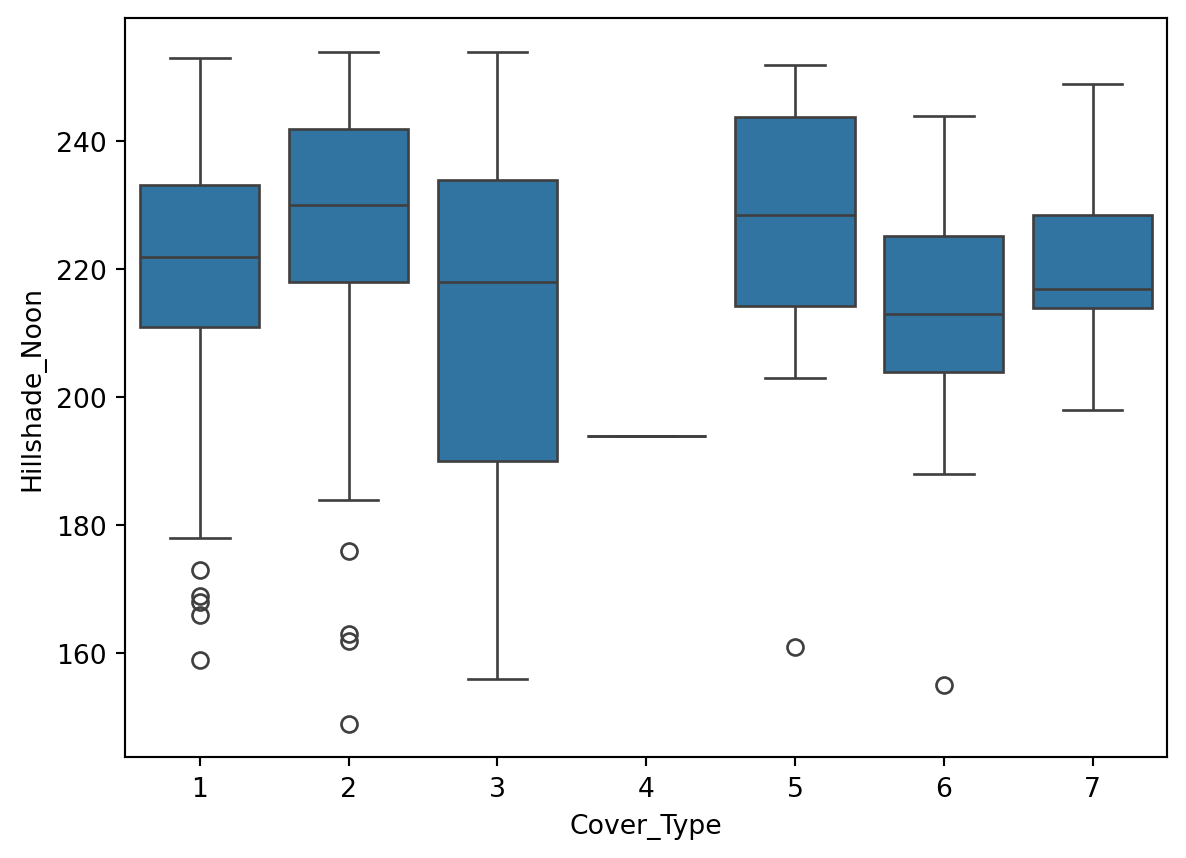
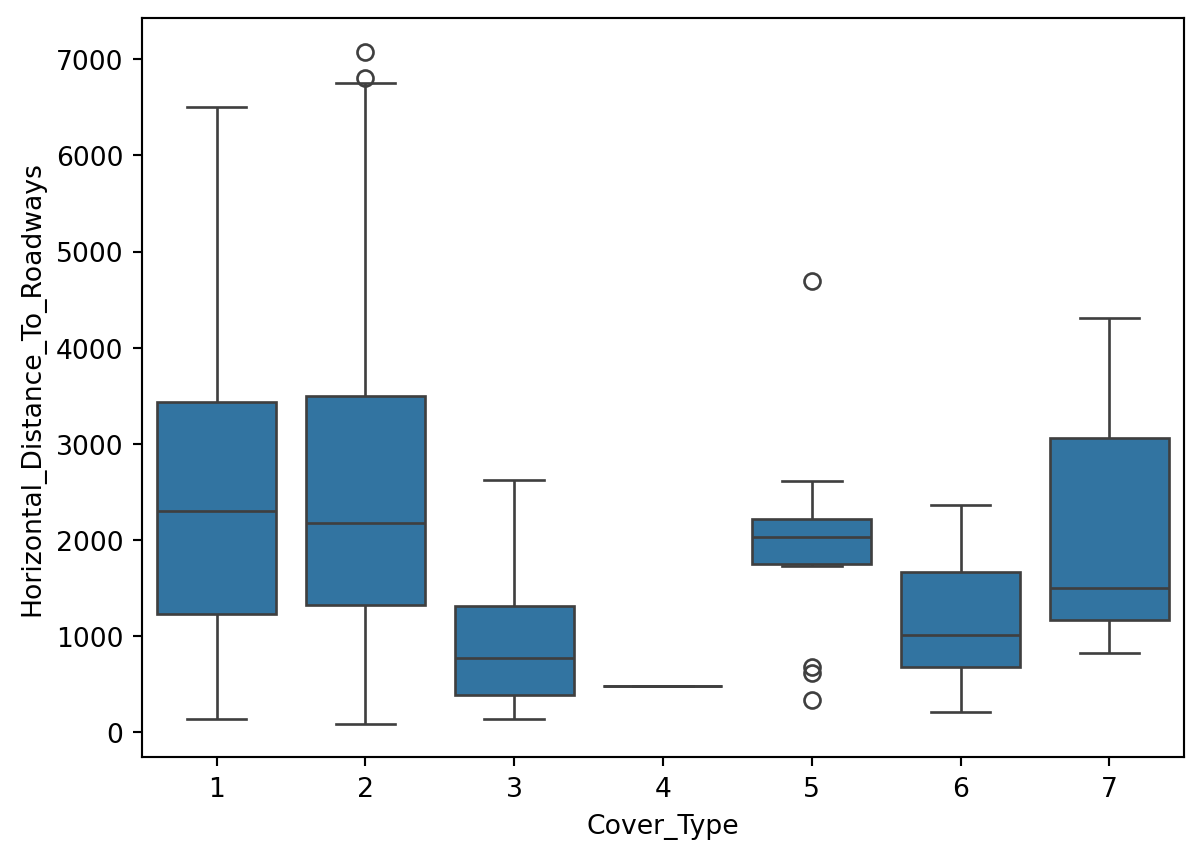
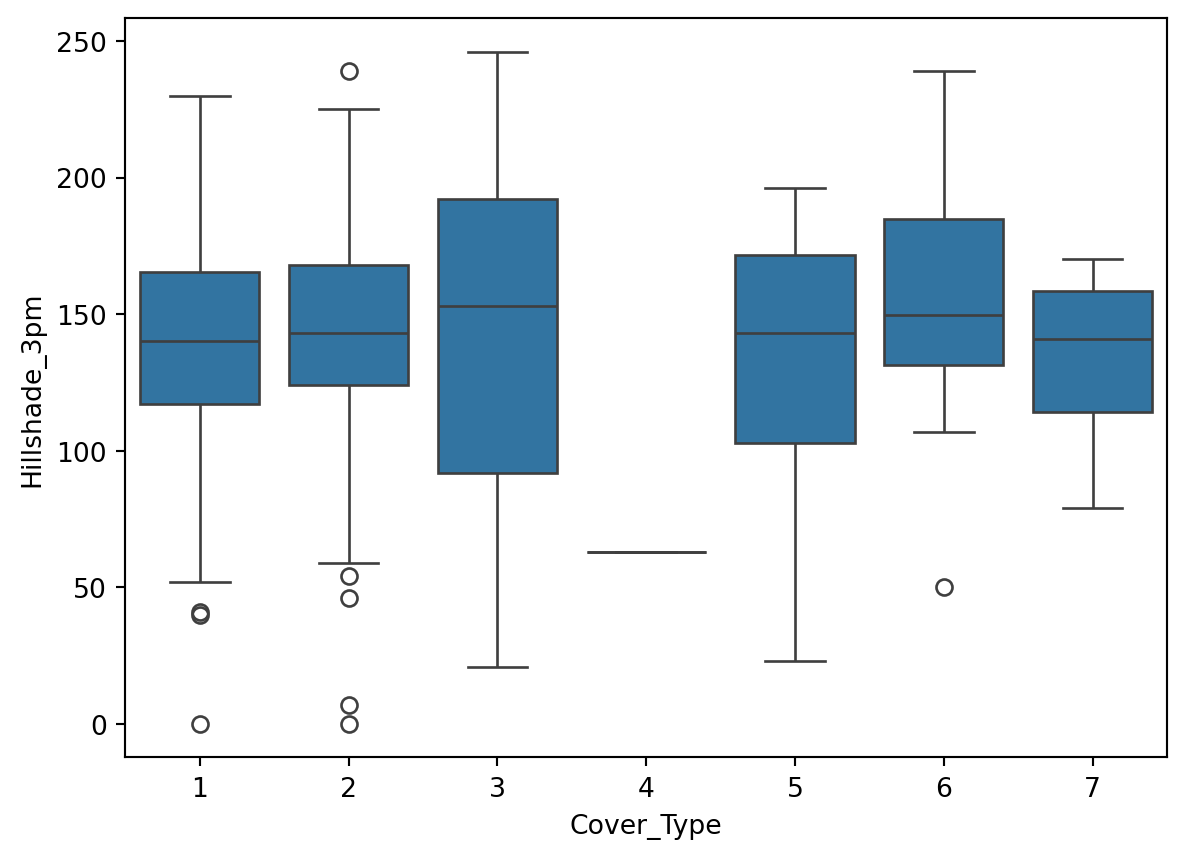
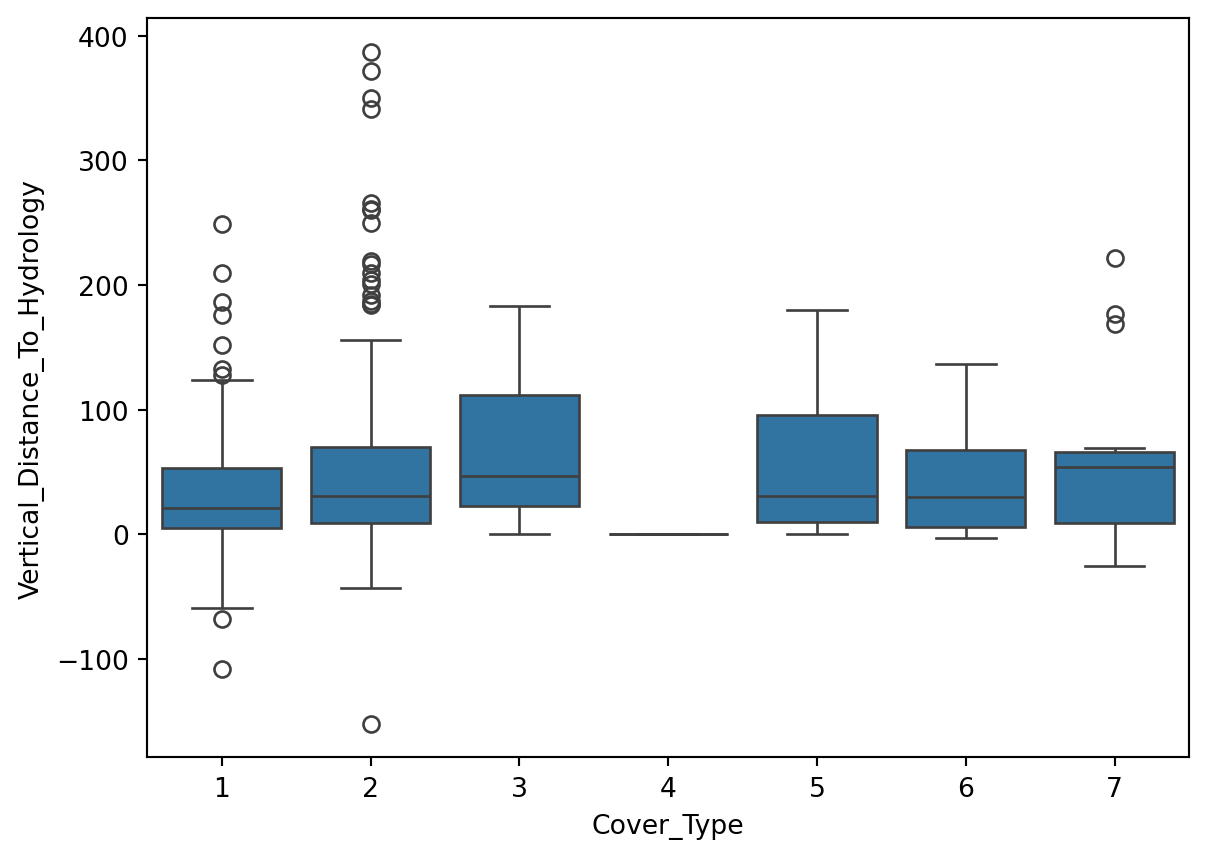
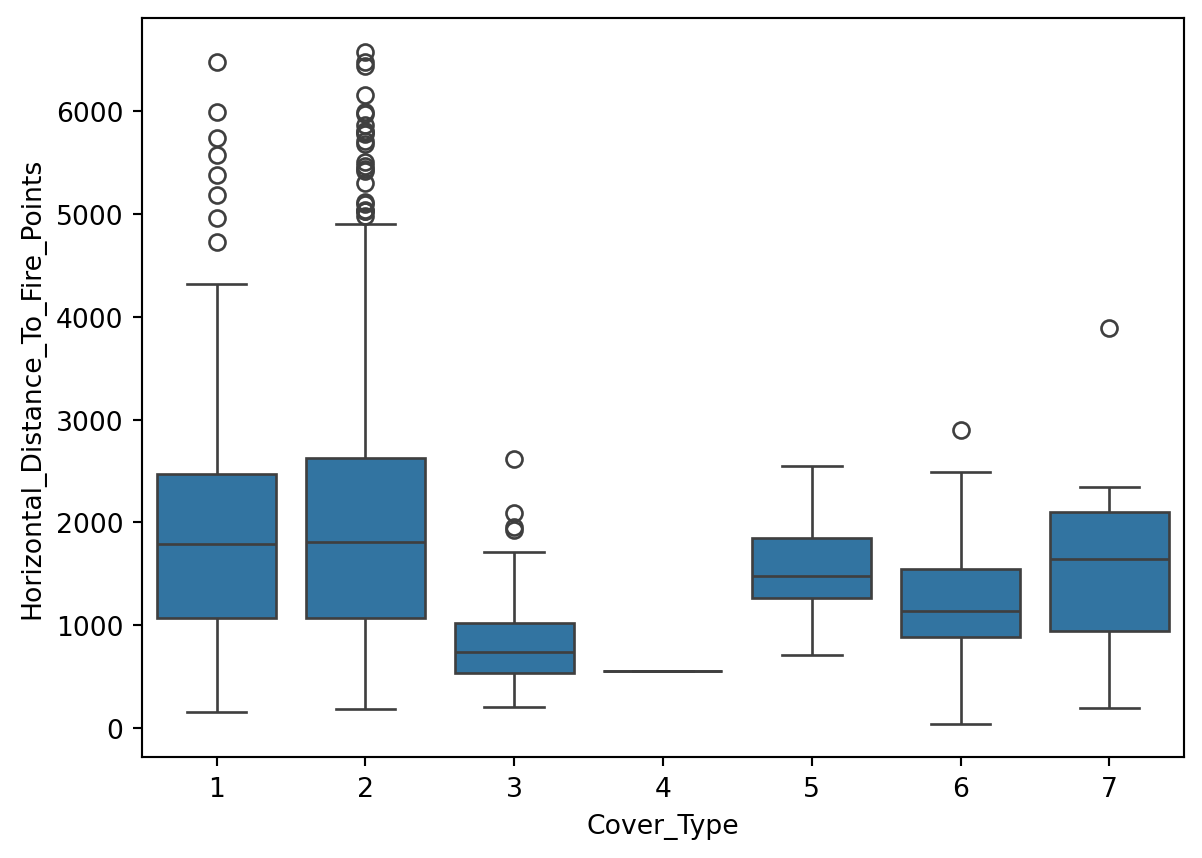
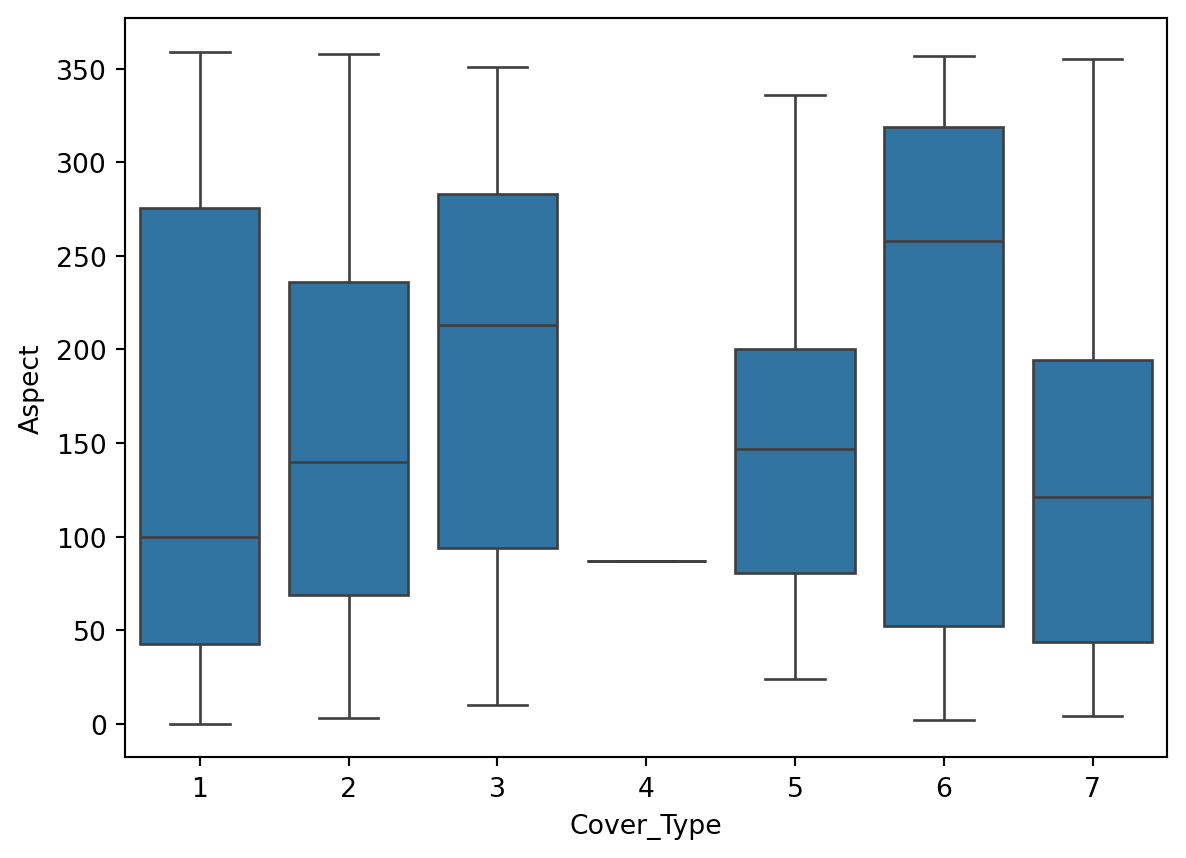
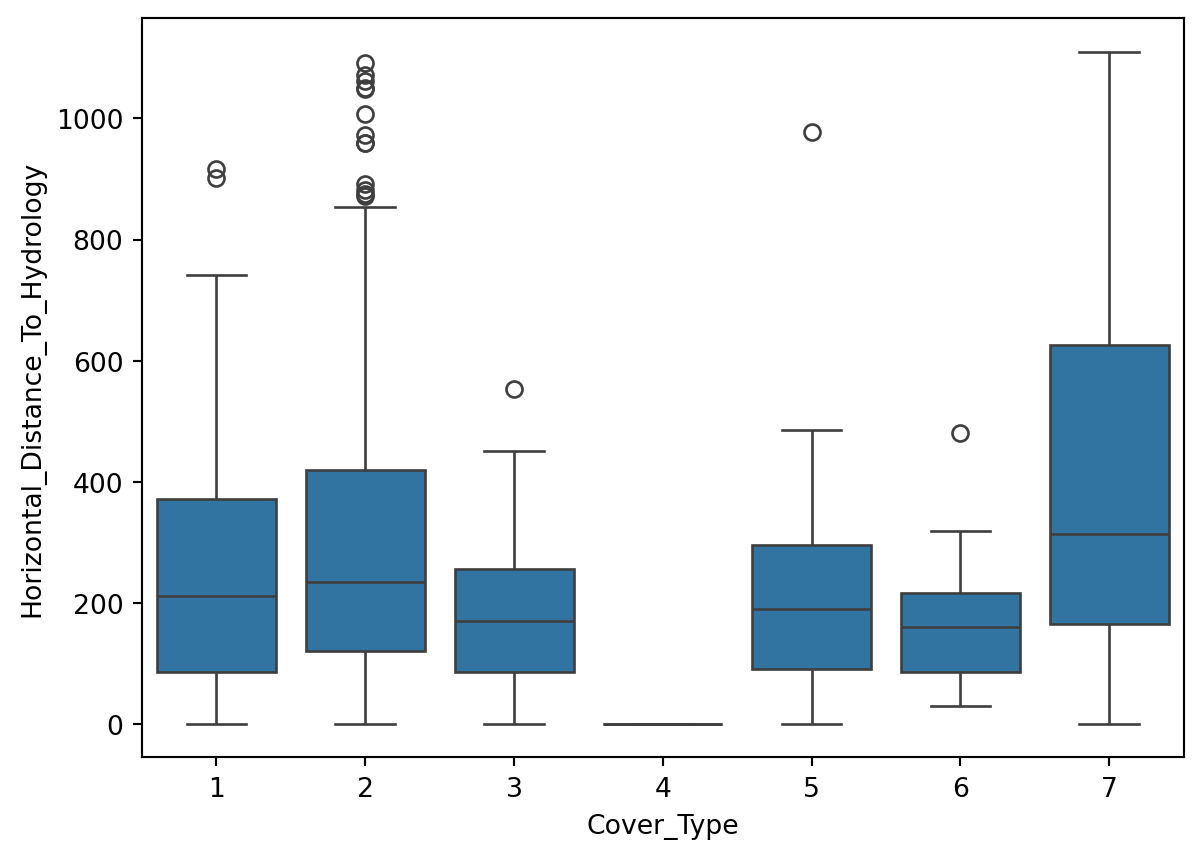
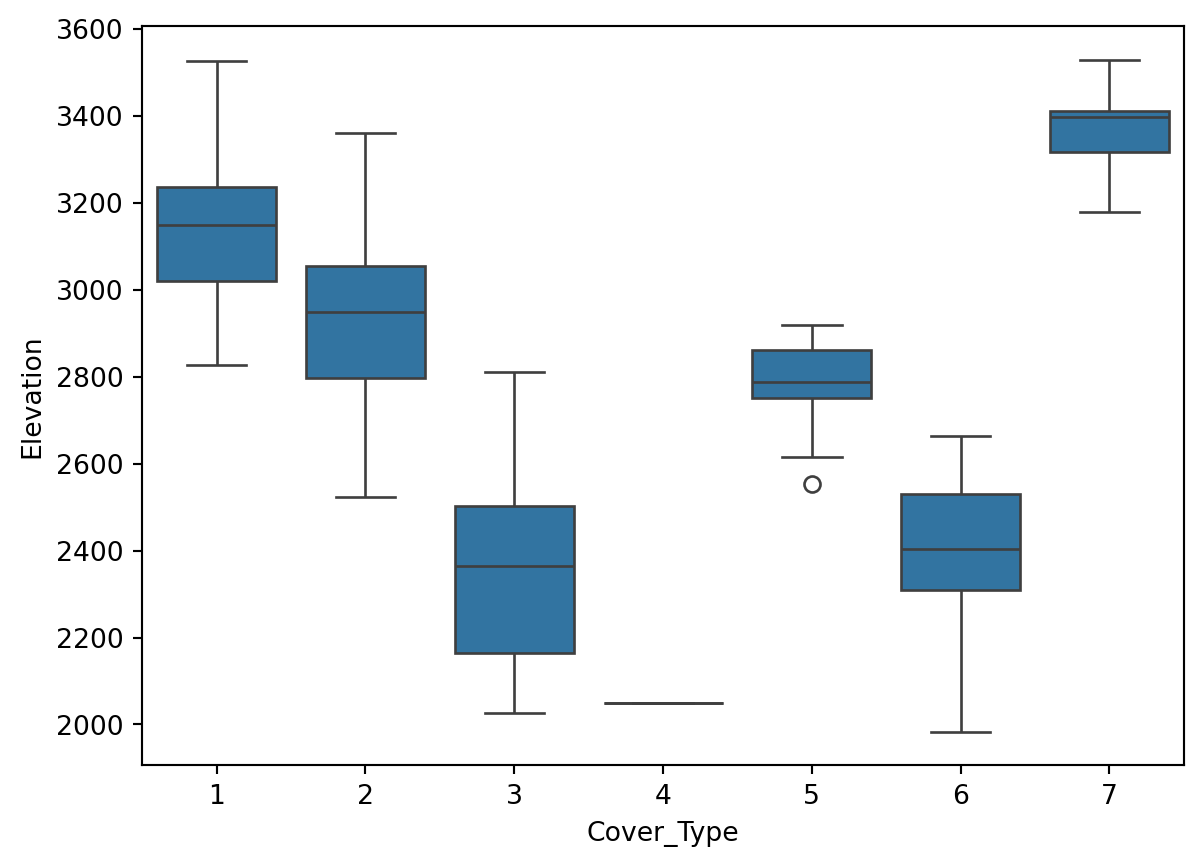
Interprétation: Nous allons nous concentrer sur la variable Elevation.

On peut voir que la variable Elevation est très discriminante.

Les types de couverture 1, 2, et 7 montrent des médianes relativement élevées pour l’élévation, avec 7 ayant la médiane la plus élevée, suivie par 1 et 2.

Chargement des données

Dataset2.

with open('Dataset2.csv', 'rb') as f:
    result = chardet.detect(f.read())  # or readline if the file is large
#print(result['encoding'])

Dataset2 = pd.read_csv('Dataset2.csv', delimiter=",",decimal = ".",encoding=result['encoding'])
Dataset2.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 581012 entries, 0 to 581011
Data columns (total 2 columns):
 #   Column           Non-Null Count   Dtype
---  ------           --------------   -----
 0   Wilderness_Area  581012 non-null  int64
 1   Soil_Type        581012 non-null  int64
dtypes: int64(2)
memory usage: 8.9 MB

Cette fois-ci, nous avons 2 variables et 581012 lignes. On peut voir que les données sont de types int64 Inspectons ces données les pour voir si elles sont numériques ou catégorielles.

# Distribution de Y
sns.countplot(x='Wilderness_Area', data=Dataset2)
plt.show()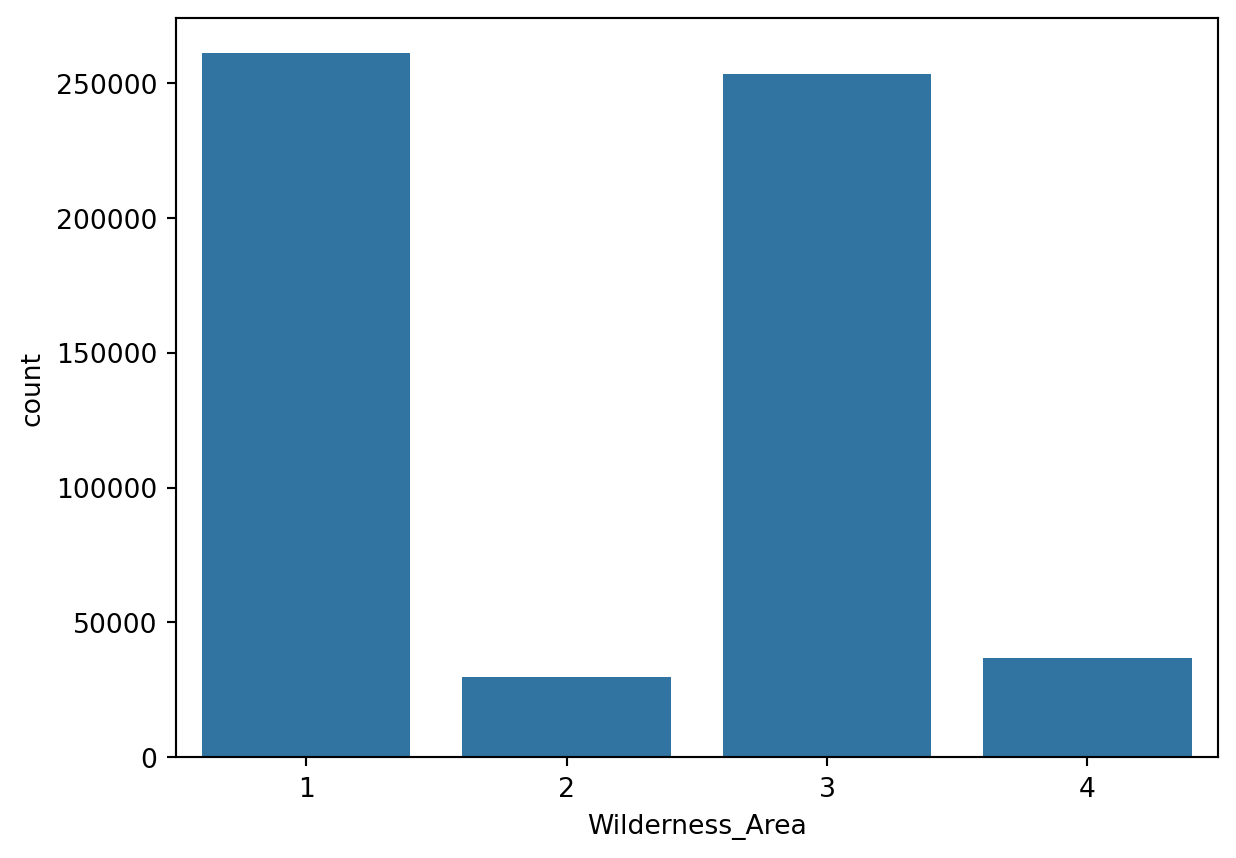

On peut voir que la variable est catégorielle. Elle contient 4 classes équilibrées. Passons à la deuxième variable.

sns.countplot(x='Soil_Type', data=Dataset2)
plt.show()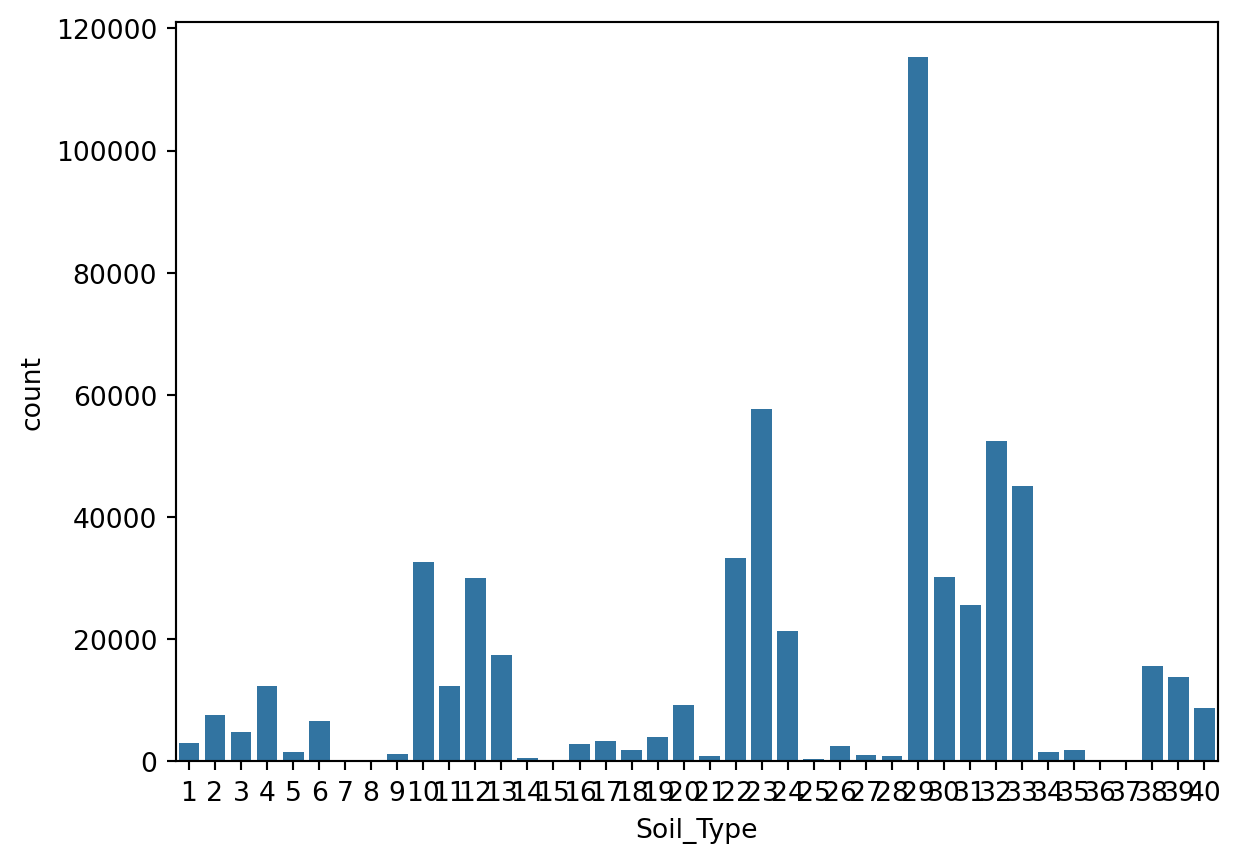

Ici, nous pouvons voir que la variable est plutôt numérique. Traçons la distribution de la variable.

_=Dataset2[['Soil_Type']].hist(figsize=(20, 14))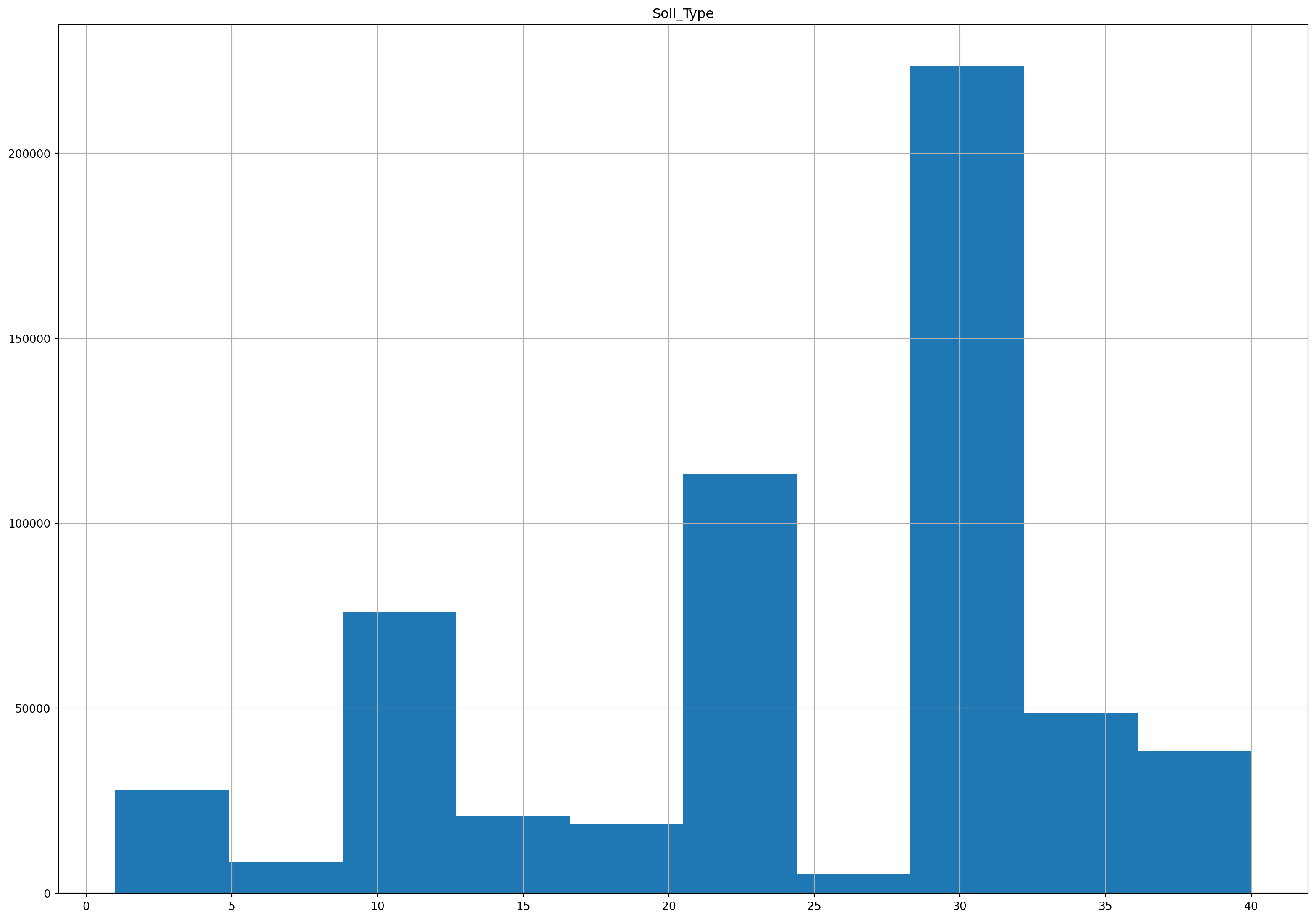

Comme les deux base de données,on les mêmes lignes, nous allons les concaténer.

combined_X = pd.concat([X, Dataset2], axis=1)
combined_X.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 581012 entries, 0 to 581011
Data columns (total 12 columns):
 #   Column                              Non-Null Count   Dtype
---  ------                              --------------   -----
 0   Slope                               581012 non-null  int64
 1   Hillshade_9am                       581012 non-null  int64
 2   Hillshade_Noon                      581012 non-null  int64
 3   Horizontal_Distance_To_Roadways     581012 non-null  int64
 4   Hillshade_3pm                       581012 non-null  int64
 5   Vertical_Distance_To_Hydrology      581012 non-null  int64
 6   Horizontal_Distance_To_Fire_Points  581012 non-null  int64
 7   Aspect                              581012 non-null  int64
 8   Horizontal_Distance_To_Hydrology    581012 non-null  int64
 9   Elevation                           581012 non-null  int64
 10  Wilderness_Area                     581012 non-null  int64
 11  Soil_Type                           581012 non-null  int64
dtypes: int64(12)
memory usage: 53.2 MB

Nous pouvons maintenant séparer les données en train et test. Avec stratification sur la variable cible.

# split  data into training and testing sets
print("Splitting data into training and testing sets...")
X_train, X_test, Y_train, Y_test = train_test_split(combined_X, Y, test_size=0.2, random_state=42, stratify=Y)

Splitting data into training and testing sets...

Avant de passer à la modélisation, nous allons standardiser les données, et encoder les variables catégorielles.

D’abord, nous allons séparer les variables numériques et catégorielles.

X_train.columns

Index(['Slope', 'Hillshade_9am', 'Hillshade_Noon',
       'Horizontal_Distance_To_Roadways', 'Hillshade_3pm',
       'Vertical_Distance_To_Hydrology', 'Horizontal_Distance_To_Fire_Points',
       'Aspect', 'Horizontal_Distance_To_Hydrology', 'Elevation',
       'Wilderness_Area', 'Soil_Type'],
      dtype='object')

categorical_cols = ['Wilderness_Area']
numerical_cols = ['Slope', 'Hillshade_9am', 'Hillshade_Noon',
       'Horizontal_Distance_To_Roadways', 'Hillshade_3pm',
       'Vertical_Distance_To_Hydrology', 'Horizontal_Distance_To_Fire_Points',
       'Aspect', 'Horizontal_Distance_To_Hydrology', 'Elevation', 'Soil_Type']

Nous allons créer un pipeline pour standardiser les données numériques et encoder les variables catégorielles. J’adore les pipelines.

numerical_transformer = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='mean')),  # or median
    ('scaler', StandardScaler())])

categorical_transformer = Pipeline(steps=[
    ('imputer', SimpleImputer(strategy='most_frequent')),
    ('onehot', OneHotEncoder(handle_unknown='ignore'))])

preprocessor = ColumnTransformer(
    transformers=[
        ('num', numerical_transformer, numerical_cols),
        ('cat', categorical_transformer, categorical_cols)])

X_train_transformed = preprocessor.fit_transform(X_train)
X_test_transformed = preprocessor.transform(X_test)

Ici nous n’avons pas de valeurs manquantes, mais nous avons quand même utilisé un imputer pour remplacer les valeurs manquantes par la moyenne pour les variables numériques et par la valeur la plus fréquente pour les variables catégorielles. Un premier pipeline pour les variables numériques et un deuxième pour les variables catégorielles. Nous avons utilisé un onehot encoder pour les variables catégorielles. Les données sont maintenant prêtes pour la modélisation.

Modélisation

Elastic Net Regression

C’est une méthode de machine learning qui combine la régression Ridge et Lasso. Elle est utilisée pour résoudre le problème de surraprentissage, la multicollinéarité et la sélection de variables.

Passons à sa modélisation :

Nous avons utilisé ici un modèle de régression logistique avec une pénalité elasticnet. Nous avons utilisé une validation croisée pour trouver le meilleur paramètre de régularisation. Nous avons utilisé une pénalité elasticnet avec un ratio de 0.5. Nous avons utilisé un solver saga qui est adapté aux problèmes multiclasse. Nous avons utilisé une tolérance de 0.01. Nous avons utilisé un random state de 12345.

clf_l1l2_LR = LogisticRegressionCV(penalty='elasticnet', l1_ratios=[0.5], 
                                   cv=5, multi_class="multinomial", 
                                 solver="saga",tol=0.01, random_state=12345)

model = Pipeline(steps=[('preprocessor', preprocessor), ('logistic', clf_l1l2_LR)])

model.fit(X_train,Y_train)
prediction = model.predict(X_test)
accuracy_LR = accuracy_score(Y_test, prediction)

print("Accuracy of Logistic Regression :","%.3f" % accuracy_LR)

Accuracy of Logistic Regression : 0.714

J’ai un accuracy de 0.714. Ce n’est pas mal. Nous pouvons voir la matrice de confusion.

# Confusion matrix

# Compute the confusion matrix
conf_matrix = confusion_matrix(Y_test, prediction)

# Display the confusion matrix using Seaborn's heatmap
plt.figure(figsize=(10, 7))
sns.heatmap(conf_matrix, annot=True, fmt='g', cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()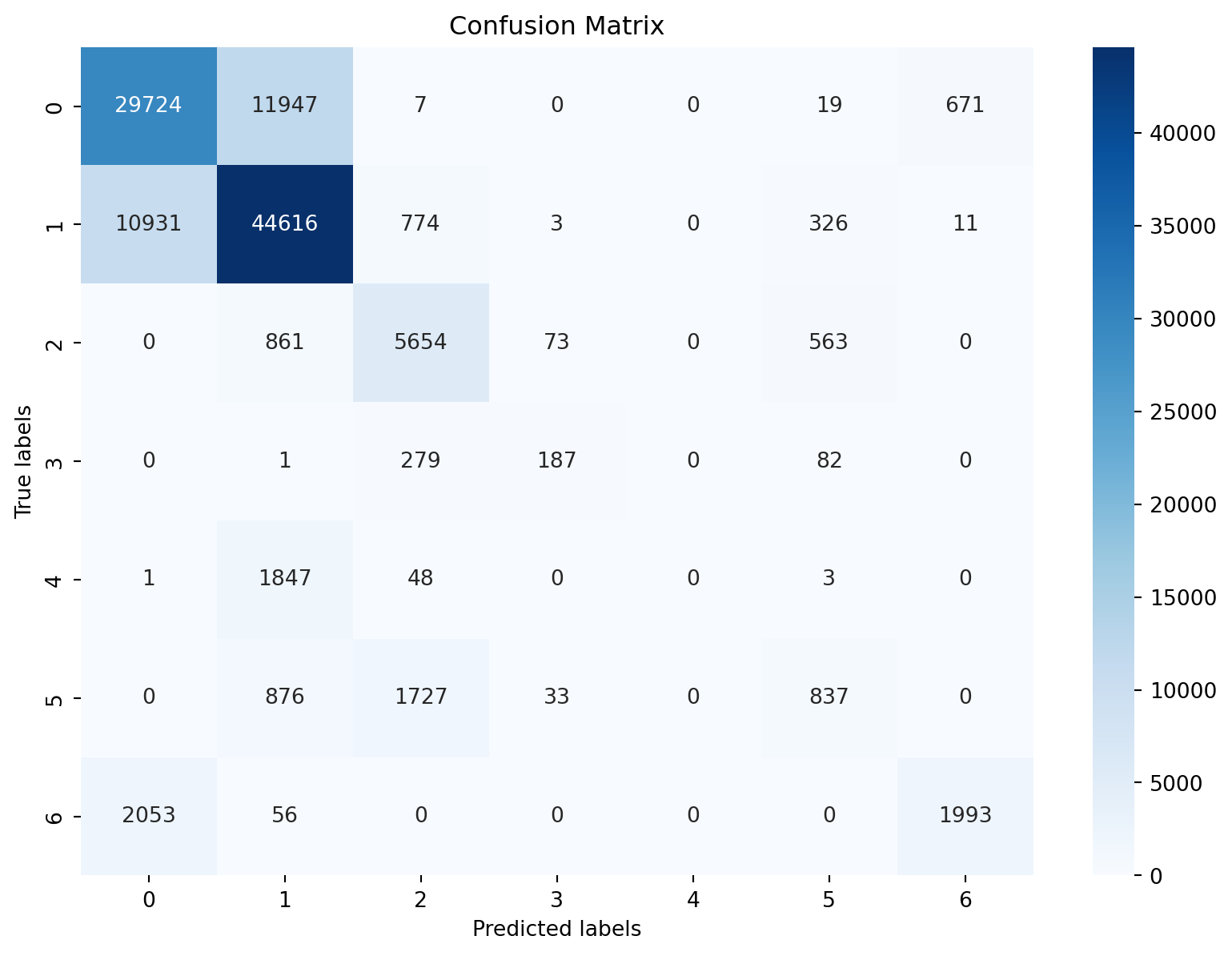

Les valeurs sur la diagonale principale (de haut à gauche à bas à droite) représentent le nombre de prédictions correctes pour chaque classe. Par exemple, il y a 29724 prédictions correctes pour la classe 0, 44616 pour la classe 1, et ainsi de suite.
Les valeurs hors de la diagonale indiquent les erreurs de classification. Par exemple, 11947 instances de la classe 0 ont été incorrectement prédites comme appartenant à la classe 1.
La classe 0 a le plus grand nombre de faux positifs, c’est-à-dire que de nombreuses instances d’autres classes ont été incorrectement prédites comme appartenant à la classe 0.
Les classes avec le moins de prédictions incorrectes (et donc les plus sombres dans la visualisation) sont la classe 3 et la classe 6, avec respectivement 187 et 1993 prédictions correctes. Les cases avec un fond plus clair, en dehors de la diagonale, indiquent des erreurs moins fréquentes entre les classes spécifiques.

Random Forest

OOB error (Out-of-bag error)

OOB est une méthode de validation croisée pour les forêts aléatoires. Chaque arbre dans la forêt est construit à partir d’un échantillon bootstrap du jeu de données d’entraînement. Certaines observations sont laissées de côté et non utilisées dans la construction d’un arbre donné. Ces observations “hors sac” peuvent être utilisées pour évaluer les performances de cet arbre. Du coup on peut utiliser cette méthode pour évaluer la performance de la forêt aléatoire et ajuster les hyperparamètres.

Le code ci-dessous montre comment calculer l’erreur OOB pour un modèle de forêt aléatoire. Il permet en particulier de sélectionner la profondeur de l’arbre dans la forêt aléatoire. Le modèle de forêt aléatoire est entraîné avec une profondeur d’arbre de 10, 20 et 30. L’erreur OOB est calculée pour chaque modèle. Le modèle avec la plus petite erreur OOB est sélectionné.

## Training Random Forest




depths = [10, 20, 30]
oob_errors = []
models = []
best_oob_error = float('inf')
best_model = None
i = 0
for depth in depths:
    print(i)
    model = RandomForestClassifier(max_depth=depth, oob_score=True, random_state=42,
                                   n_estimators=100,  
                                   warm_start=True  # This allows us to add more estimators later if needed
                                  )
    model.fit(X_train, Y_train)
    oob_error = 1 - model.oob_score_
    oob_errors.append(oob_error)
    models.append(model)
    if oob_error < best_oob_error:
        best_oob_error = oob_error
        best_model = model
    i = i+1
    print("Done")

# Print OOB errors for each model
for depth, error in zip(depths, oob_errors):
    print(f"Depth: {depth}, OOB Error: {error}")

0
Done
1
Done
2
Done
Depth: 10, OOB Error: 0.21680518234371537
Depth: 20, OOB Error: 0.05706860237215716
Depth: 30, OOB Error: 0.038628770096964526

Accuracy et matrice de confusion

# Compute the accuracy of the best random forest model
predictions = best_model.predict(X_test)
accuracy = accuracy_score(Y_test, predictions)
print("Accuracy of the Best Random Forest: {:.3f}".format(accuracy))

# Display the confusion matrix
conf_matrix = confusion_matrix(Y_test, predictions)
plt.figure(figsize=(10, 7))
sns.heatmap(conf_matrix, annot=True, fmt='g', cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()

Accuracy of the Best Random Forest: 0.962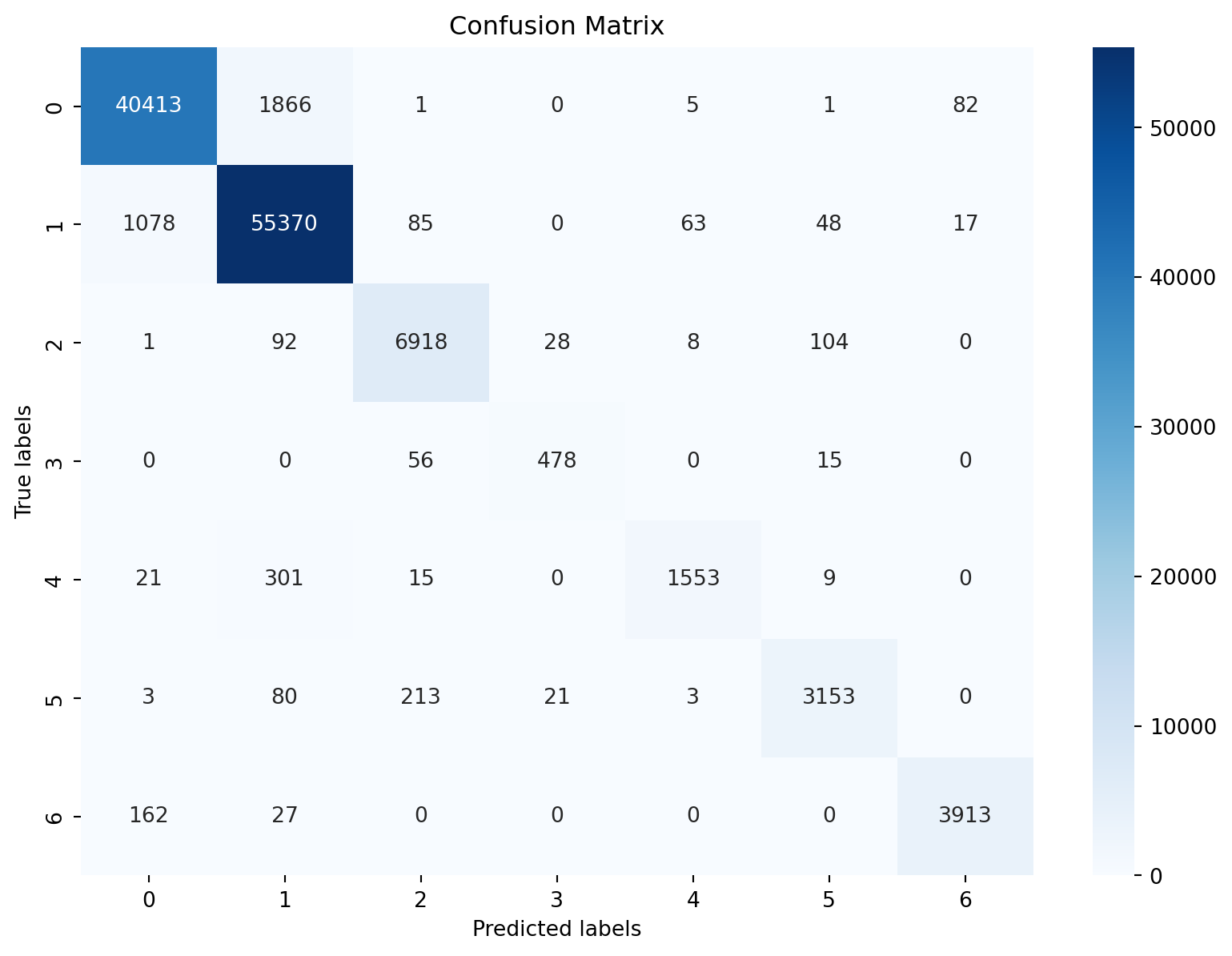

Nous avons un accuracy de 0.962. C’est très bien si on compare avec le modèle de régression logistique qui a un accuracy de 0.714. Nous pouvons voir la matrice de confusion.

Xgboost

Essayons tout d’abord par expliquer ce qu’est le Xgboost. Xgboost signifie Extreme Gradient Boosting. Il combine des weaks models afin de produire des prédictions plus précises. Il est très rapide et performant.

Avant de passer à la modélisation, il faut transformer les données en un format spécifique à Xgboost. En effet, le package xgboost ne gère pas les chaînes de caractères pour les étiquettes contrairement à tous les modèles entraînés précédemment, donc vous devez d’abord les encoder en tant qu’entiers. De plus, il encode automatiquement les étiquettes en tant que 0, 1, 2, etc. Cela signifie que si vous avez des étiquettes de classe 1, 2, 3, 4, 5, 6, 7, vous devez les encoder en tant que 0, 1, 2, 3, 4, 5, 6. Il faut le faire pour les labels(Y_train et Y_test) d’entraînement et de test.

# encode string class values as integers


label_encoder = LabelEncoder()
label_encoder = label_encoder.fit(Y)
label_encoded_y_train = label_encoder.transform(Y_train)
label_encoded_y_test = label_encoder.transform(Y_test)

# Vérifiez les étiquettes uniques dans les ensembles d'entraînement et de test
unique_train_labels = np.unique(label_encoded_y_train)
unique_test_labels = np.unique(label_encoded_y_test)

print("Unique labels in training set:", unique_train_labels)
print("Unique labels in test set:", unique_test_labels)

Unique labels in training set: [0 1 2 3 4 5 6]
Unique labels in test set: [0 1 2 3 4 5 6]

Nous avons utilisé un modèle de classification Xgboost avec les paramètres suivants:

objective=‘multi:softprob’ : Spécifie la fonction objectif de l’entraînement. Ici, ‘multi:softprob’ est utilisé pour les problèmes de classification multiclasse et retournera une matrice de probabilité estimée pour chaque classe, ce qui est nécessaire pour calculer des scores comme le log-loss.
seed=‘12345’ : Fournit une graine pour le générateur de nombres aléatoires. Cela garantit que les résultats sont reproductibles. Toutefois, il semble y avoir une petite confusion ici, car la graine devrait être un entier (seed=12345), pas une chaîne de caractères (seed=‘12345’).
gamma=0 : Paramètre de régularisation qui minimise la complexité du modèle et aide à prévenir le surajustement. La valeur de 0 indique qu’il n’y a pas de régularisation supplémentaire.
learning_rate=0.05 : C’est le taux d’apprentissage, également connu sous le nom d’eta. Cela contribue à rendre le processus d’apprentissage plus robuste en empêchant les poids de s’ajuster trop fortement à chaque itération. Une valeur plus faible peut nécessiter plus d’arbres pour apprendre les mêmes relations, mais peut améliorer la performance finale du modèle.
max_depth=5 : Détermine la profondeur maximale de chaque arbre. C’est un autre paramètre qui aide à prévenir le surajustement. Plus la profondeur est grande, plus le modèle est complexe.
n_estimators=200 : Le nombre d’arbres à construire. Plus il y a d’arbres, plus le modèle peut être précis, mais cela augmente aussi le temps de calcul et le risque de surajustement.

clf_xgb = XGBClassifier(objective='multi:softprob', seed='12345',
                       gamma=0, learning_rate=0.05, max_depth=5, n_estimators=200,num_class=7)
clf_xgb.fit(X_train, label_encoded_y_train)

accuracy_xgb = accuracy_score(label_encoder.transform(Y_test), clf_xgb.predict(X_test))

print("Accuracy of XGBOOST :","%.3f" % accuracy_xgb)

Accuracy of XGBOOST : 0.786

Ici on a un accuracy de 0.0.786. C’est mieux que le modèle de régression logistique mais moins bien que le modèle de forêt aléatoire. Nous pouvons voir la matrice de confusion.

# Display the confusion matrix
predictions = clf_xgb.predict(X_test)
conf_matrix = confusion_matrix(label_encoded_y_test, predictions)
plt.figure(figsize=(10, 7))
sns.heatmap(conf_matrix, annot=True, fmt='g', cmap='Blues')
plt.title('Confusion Matrix')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()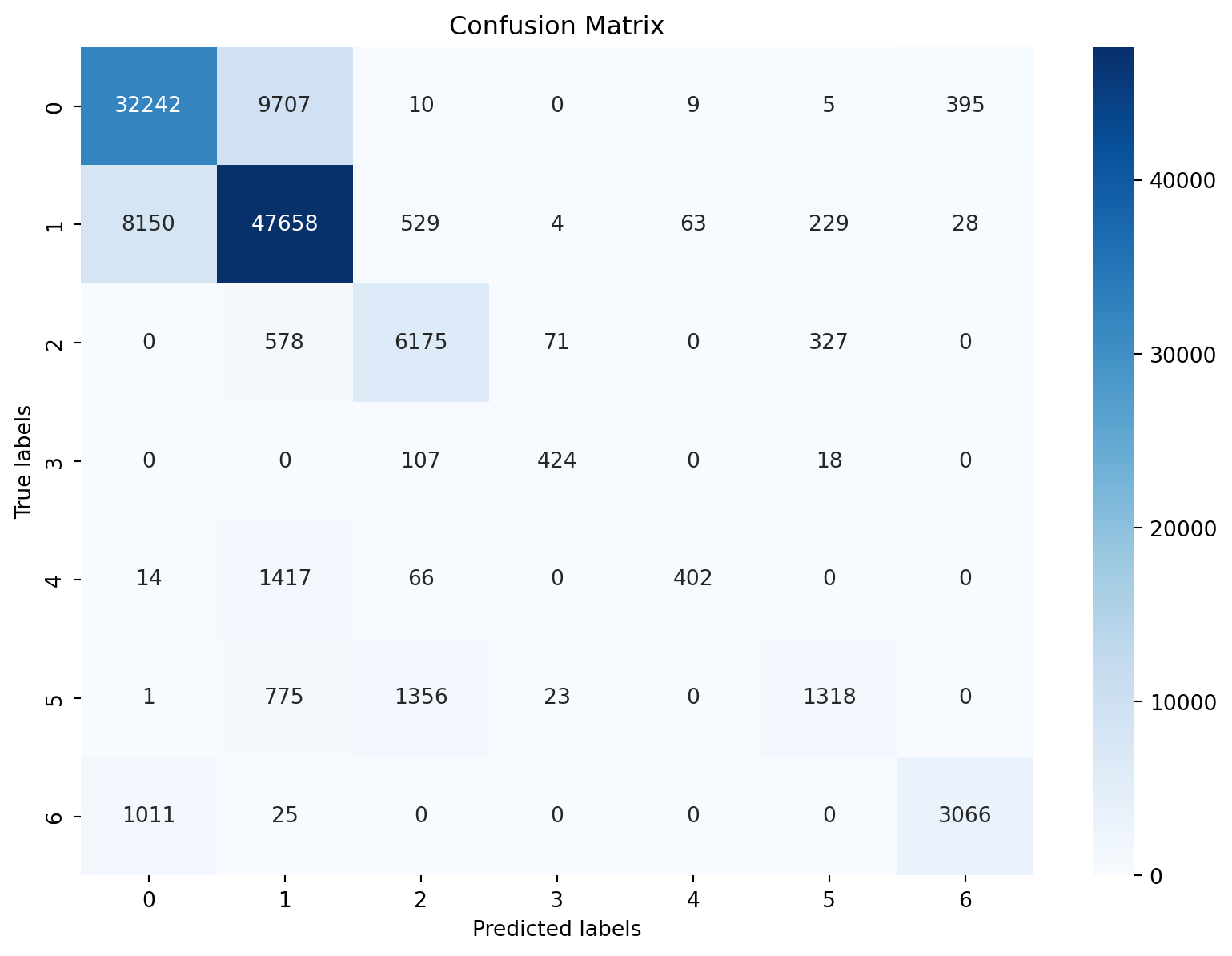

Courbe ROC

La courbe ROC est un graphique qui montre la performance d’un modèle de classification à différents seuils de classification. Elle trace le taux de vrais positifs (TPR) en fonction du taux de faux positifs (FPR) à différents seuils de classification. Le TPR est également connu sous le nom de rappel et le FPR est égal à 1 - spécificité.

import numpy as np
from sklearn.preprocessing import label_binarize
from sklearn.metrics import roc_curve, auc

def compute_roc_auc(models, X, Y_test):
    """
    Compute ROC AUC for a list of models.
    
    Args:
    models (dict): A dictionary of models with their names as keys.
    X_test (array-like): Test features.
    Y_test (array-like): True labels for the test set.
    
    Returns:
    dict: A dictionary containing FPR, TPR, and ROC AUC for each model.
    """
    Y_classes = np.unique(Y_test)
    Y_test_binarized = label_binarize(Y_test, classes=Y_classes)
    n_classes = len(Y_classes)
    
    results = {}

    for model_name, model in models.items():
        if model_name == 'Logistic':
            model = Pipeline(steps=[('preprocessor', preprocessor), ('logistic', clf_l1l2_LR)])
            model.fit(X_train,Y_train)
            score = model.predict_proba(X_test)
        else:
          
            score = model.predict_proba(X_test)
        
        fpr = dict()
        tpr = dict()
        roc_auc = dict()

        # Compute ROC for each class
        for i in range(n_classes):
            fpr[i], tpr[i], _ = roc_curve(Y_test_binarized[:, i], score[:, i])
            roc_auc[i] = auc(fpr[i], tpr[i])

        # Compute micro-average ROC curve and ROC area
        fpr["micro"], tpr["micro"], _ = roc_curve(Y_test_binarized.ravel(), score.ravel())
        roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

        results[model_name] = {'fpr': fpr, 'tpr': tpr, 'roc_auc': roc_auc, 'score':score}

    return results

models = {
    'Logistic': clf_l1l2_LR,
      # Assurez-vous que clf_svm est entraîné sur des données mises à l'échelle si nécessaire
    'Random Forests': best_model,
    'XGBOOST': clf_xgb,
    
}

roc_results = compute_roc_auc(models, X_test, Y_test)

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k--')  # Ligne diagonale

for model_name, metrics in roc_results.items():
    plt.plot(metrics['fpr']['micro'], metrics['tpr']['micro'], label=f'{model_name} Micro (area = {metrics["roc_auc"]["micro"]:.2f})')

plt.legend()
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title('Micro-Average Receiver Operating Characteristic')
plt.show()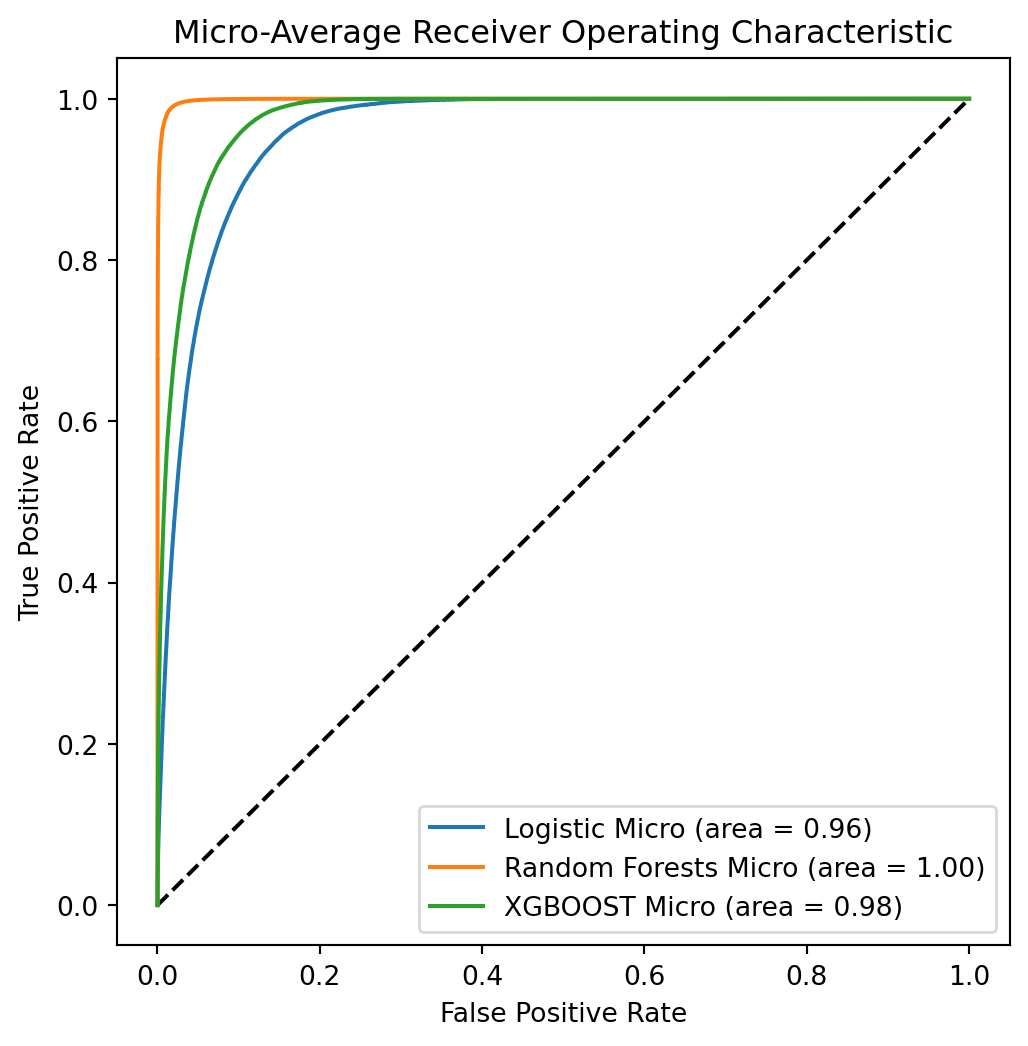

La courbe ROC montre que le modèle de forêt aléatoire est le meilleur modèle. Il a la plus grande surface sous la courbe (AUC). Le modèle Xgboost est le deuxième meilleur modèle. Le modèle de régression logistique est le moins bon modèle.

Bonus

from sklearn.metrics import roc_auc_score

# Affichage des AUC micro-averaged
print("Area under Roc Curve (micro-average) for:\n")
for model_name in models.keys():
    print(f"- {model_name}: {roc_results[model_name]['roc_auc']['micro']:.3f}")

# Calcul et affichage des AUC one-vs-one macro-averaged
print("\nArea under Roc Curve (one-vs-one macro-average) for:\n")
for model_name, model in models.items():
    
    score = roc_results[model_name]['score']
    auc_ovo_macro = roc_auc_score(Y_test, score, multi_class="ovo", average="macro")
    print(f"- {model_name}: {auc_ovo_macro:.3f}")

Area under Roc Curve (micro-average) for:

- Logistic: 0.959
- Random Forests: 0.999
- XGBOOST: 0.977

Area under Roc Curve (one-vs-one macro-average) for:

- Logistic: 0.917
- Random Forests: 0.998
- XGBOOST: 0.966

Conclusion

Pour aborder cet exercice de manière efficace, je vous recommande fortement de vous concentrer sur la préparation préalable de vos propres fonctions, plutôt que de vous reposer excessivement sur des générateurs de texte automatiques. La création de vos fonctions en amont vous permettra de gagner un temps précieux. N’oubliez pas que les fonctions et les pipelines que vous avez déjà utilisés ont été préparés avant même de commencer le devoir ; votre tâche consiste essentiellement à les adapter aux besoins spécifiques de la situation.

Par ailleurs, l’utilisation judicieuse de ChatGPT peut s’avérer très bénéfique, notamment dans des tâches telles que la génération de boxplots ou l’implémentation de l’algorithme pour calculer l’erreur out-of-bag (Out-of-bag error). ChatGPT peut fournir des conseils, des exemples de code ou des explications qui peuvent faciliter le processus de développement. Cependant, gardez à l’esprit que l’outil doit être utilisé comme un complément à votre propre travail de programmation et de réflexion, et non comme une solution complète.